• A new real-time PCR method to overcome significant quantitative inaccuracy due to slight amplification inhibition

    Abstract

    Background: Real-time PCR analysis is a sensitive DNA quantification technique that has recently gained considerable attention in biotechnology, microbiology and molecular diagnostics. Although, the cycle-threshold (Ct) method is the present "gold standard", it is far from being a standard assay. Uniform reaction efficiency among samples is the most important assumption of this method. Nevertheless, some authors have reported that it may not be correct and a slight PCR efficiency decrease of about 4% could result in an error of up to 400% using the Ct method. This reaction efficiency decrease may be caused by inhibiting agents used during nucleic acid extraction or copurified from the biological sample. We propose a new method (Cy0) that does not require the assumption of equal reaction efficiency between unknowns and standard curve.
    Results: The Cy0 method is based on the fit of Richards' equation to real-time PCR data by nonlinear regression in order to obtain the best fit estimators of reaction parameters. Subsequently, these parameters were used to calculate the Cy0 value that minimizes the dependence of its value on PCR kinetic.
    The Ct, second derivative (Cp), sigmoidal curve fitting method (SCF) and Cy0 methods were compared using two criteria: precision and accuracy. Our results demonstrated that, in optimal amplification conditions, these four methods are equally precise and accurate. However, when PCR efficiency was slightly decreased, diluting amplification mix quantity or adding a biological inhibitor such as IgG, the SCF, Ct and Cp methods were markedly impaired while the Cy0 method gave significantly more accurate and precise results.

    Conclusion: Our results demonstrate that Cy0 represents a significant improvement over the standard methods for obtaining a reliable and precise nucleic acid quantification even in sub-optimal amplification conditions overcoming the underestimation caused by the presence of some PCR inhibitors.

    free_upload

    Hello, You are the visitor, Thanks.

    Visiting us from ...

    visitors location 
    

    
Warning:  mysqli_real_escape_string() expects parameter 1 to be mysqli, boolean given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 43
    

    
Notice:  Only variables should be passed by reference in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 44
    

    
Warning:  mysqli_query() expects parameter 1 to be mysqli, boolean given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 65
    

    
Warning:  mysqli_num_rows() expects parameter 1 to be mysqli_result, null given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 66
    

    
Warning:  mysqli_fetch_assoc() expects parameter 1 to be mysqli_result, null given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 68
    

    
Warning:  mysqli_query() expects parameter 1 to be mysqli, boolean given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 85
    

    
Warning:  mysqli_num_rows() expects parameter 1 to be mysqli_result, null given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 86
    
    
    latest clicks ... 
    
    
    
Warning:  mysqli_query() expects parameter 1 to be mysqli, boolean given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 150
    

    
Warning:  mysqli_num_rows() expects parameter 1 to be mysqli_result, null given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 157
    

    
Warning:  mysqli_fetch_array() expects parameter 1 to be mysqli_result, null given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 163
    

    
Warning:  mysqli_close() expects parameter 1 to be mysqli, boolean given in /home/cymethod/domains/cy0method.org/public_html/navigation/last_5_clicks.php on line 174
    
                      
    

                      
                    

                 
                     
                 
    

  
                   
    




      

                
    Background
    

                In the last few years, the real-time
                polymerase chain reaction (PCR) has rapidly become the most widely used technique
                in modern molecular biology [1-4].
    
                This technique relies on fluorescence-based detection of amplicon DNA and allows the kinetics of PCR
                amplification to be monitored in real time, making it possible to quantify
                nucleic acids with extraordinary ease and precision. With a large dynamic range
                (7-8 magnitudes) and a high degree of sensitivity (5-10 molecules), the real-time
                PCR addresses the evident requirement for quantitative data analysis in
                molecular medicine, biotechnology, microbiology and diagnostics  [
                5, 6].

                Although, the real-time PCR analysis
                has gained considerable attention in many fields of molecular biology, it is
                far from being a standard assay. One of the problems associated with this assay,
                which has a direct impact on its reliability, is inconsistent data analysis. At
                the present, real-time PCR analysis is highly subjective and, if carried out
                inappropriately, confuses the actual results [7].

                Many different options for data processing are currently available.
                The basic choice in real time PCR
                calculations is between absolute quantification, based on standard curve, and
                relative quantification, based on PCR efficiency calculation. Using the
                software currently available, analysis of real-time PCR data is generally based
                on the  "cycle-threshold
                " method. The cycle-threshold
                is defined as the fractional cycle number in the log-linear region of PCR
                amplification in which the reaction reaches fixed amounts of amplicon DNA.
                There are two methods for determining the cycle-threshold value; one method,
                namely fit point, is performed by drawing a line parallel to the x-axis of the
                real-time fluorescence intensity curve (Ct) [8]. The second, namely second
                derivative, calculates the fractional cycle where the second derivative of the
                real-time fluorescence intensity curve reaches the maximum value (Cp) [9].
                Standard curve method requires
                generating serial dilutions of a given sample and performing multiple PCR
                reactions on each dilution [10, 11], the threshold-cycle values are
                then plotted versus the log of the dilution and a linear regression is performed
                from which the mean efficiency can be derived. This approach is only valid if
                the threshold-cycle values are measured from the exponential phase of the PCR
                reaction and if the efficiency is identical between amplifications.
                Furthermore, this efficiency is assumed to be the same for all the standard
                dilutions, but some authors have reported that this assumption may be
                questionable [12].

                It is well-recognized that template quality is one of the most important
                determinants of real-time PCR reliability and reproducibility [13], and numerous authors have shown the
                significant reduction in the sensitivity and kinetics of real-time PCR assays
                caused by inhibitory components frequently found in biological samples [14, 17].
                The inhibiting agents may be
                reagents used during nucleic acid extraction or copurified components from the
                biological sample such as bile salts, urea, haeme, heparin, and immunoglobulin
                G. Inhibitors can generate strongly inaccurate quantitative results; while, a
                high degree of inhibition may even create false-negative results.

                The Ct method is the most widely used method even though its
                calculation is user-dependent. The Ct
                method is quite stable and straightforward but the accuracy of estimates is strongly
                impaired if efficiency is not equal in all reactions. Indeed, uniform reaction
                efficiency is the most important assumption of the Ct method.

                An alternative approach, proposed by
                Liu and Saint [18], assumes a dynamic change in
                efficiency fitting PCR amplification with a sigmoid function (Sigmoidal curve
                fitting method, SCF). One of
                the advantages of this regression analysis is that it allows us to estimate the
                initial template amount directly from the non-linear regression, eliminating
                the need for a standard curve. These pioneering works showed that it was
                possible to obtain absolute quantification from real-time fluorescence curve
                shape. However, recent reports have demonstrated that, in an optimized assay,
                the Ct method remains the gold
                standard due to the inherent errors of the multiple estimates used in
                non-linear regression [19, 20].

                We propose, in this report, a
                modified standard curve-based method (named Cy0)
                that does not require the assumption of uniform reaction efficiency between
                standards and unknown and does not involve any choice of threshold level by the
                user.

                The aim of this work was also to compare
                the accuracy and precision of the SCF,
                Ct, Cp and Cy0
                methods in presence of varying PCR kinetics. Our results clearly show that the
                proposed data processing procedure can effectively be applied in the
                quantification of samples characterized by slight amplification inhibition
                obtaining reliable and precise results.


                
    Methods
    


                
    Experimental design
    

                The absolute quantification method
                relies on the comparison of distinct samples, such as the comparison of a
                biological sample with a standard curve of known initial concentration [21].
    
                We wondered how accuracy and
                precision change when a standard curve is compared with unknown samples characterized
                by different efficiencies. A natural way of studying the effect of efficiency
                differences among samples on quantification would be to compare the amounts of
                a quantified gene.
    

                A slight amplification inhibition in
                the quantitative real-time PCR experiments was obtained by using two systems:
                decreasing the amplification mix used in the reaction and adding varying amounts
                of IgG, a known PCR inhibitor.
    

                For the first system, we amplified
                the MT-ND1 gene by real-time PCR in reactions having the same initial amount of
                DNA but different amounts of SYBR Green I Master mix. A standard curve was performed over a wide range of input
                DNA (3.14x107-3.14x101) in the presence of optimal
                amplification conditions (100% amplification mix), while the unknowns were run
                in the presence of the same starting DNA amounts but with amplification mix
                quantities ranging from 60% to 100%. This
                produced different reaction kinetics, mimicking the amplification
                inhibition that often occurs in biological samples [17, 22].
    

                Furthermore, quantitative real-time
                PCR quantifications were performed in the presence of an optimal amplification
                reaction mix added with serial dilutions of IgG (0.0625 - 2 µg/ml) thus acting as the inhibitory
                agent [23].

       
    



                The reaction efficiency obtained was estimated by the LinReg method [24]. This approach
                identifies the exponential phase of the reaction by plotting the fluorescence
                on a log scale. A linear regression is then performed leading to the estimation
                of the efficiency of each PCR reaction.


                
    Quantitative Real-Time PCR
    


                The DNA standard consisted of a
                pGEM-T (Promega) plasmid containing a 104 bp fragment of the mitochondrial gene
                NADH dehydrogenase 1 (MT-ND1) as insert. This DNA fragment was produced by the
                ND1/ND2 primer pair (forward ND1: 5 ' -ACGCCATAAAACTCTTCACCAAAG-3
                '  and reverse ND2: 5 ' -TAGTAGAAGAGCGATGGTGAGAGCTA-3
                ' ). This plasmid was purified using the Plasmid Midi Kit (Qiagen)
                according to the manufacturer ' s instructions. The final concentration
                of the standard plasmid was estimated spectophotometrically by averaging three
                replicate A260 absorbance determinations.

                Real time PCR amplifications were
                conducted using LightCycler®
                480 SYBR Green I Master (Roche) according to the manufacturer's
                instructions, with 500 nM primers and a variable amount of DNA standard in a 20µl final reaction volume.
                Thermocycling was conducted using a LightCycler®
                480 (Roche) initiated by a 10 min incubation at 95°C, followed by 40 cycles
                (95°C for 5 s; 60°C for 5 s; 72°C for 20 s) with a single fluorescent reading
                taken at the end of each cycle. Each reaction combination, namely starting DNA
                and amplification mix percentage, was conducted in triplicate and repeated in
                four separate amplification runs. All the runs were completed with a melt curve
                analysis to confirm the specificity of amplification and lack of primer dimers.
                Ct (fit point method) and Cp
                (second derivative method) values were determined by the LightCycler® 480
                software version 1.2 and exported into an MS Excel data sheet (Microsoft) for analysis after background
                subtraction (available as Additional file 1). For Ct (fit point method) evaluation a fluorescence threshold
                manually set to 0.5 was used for all runs.

                
    Description of the SCF method
    

                Fluorescence readings were used to fit the following 4-parameter sigmoid function using nonlinear regression
                analysis:

                
                
    
                    
    
                        
                            

                        
                        Eq. 1
                    
    


                where x is the cycle number, Fx
                is the reaction fluorescence at cycle x,
                Fmax is the maximal
                reaction fluorescence, c is the
                fractional cycle at which reaction fluorescence reaches half of Fmax,
                b is related to the slope of the curve and Fb is the background
                reaction fluorescence. Fmax quantifies the maximal
                fluorescence read by the instrument and does not necessarily indicate the
                amount of DNA molecules present at the end of the reaction. The fact that Fmax
                 does not necessarily represent the final amount of DNA might be due to un-saturating dye
                concentration or to fluorescence quenching by inhibitors. For each run a
                nonlinear regression analysis was performed and these four parameters were
                evaluated. A simple derivative of Eq. 1 allowed us to estimate F0,
                when x = 0:

                
                
    
                    
    
                        
                            

                        
                        Eq. 2
                    
    

                where F0 represents the initial target quantity expressed in
                fluorescence units. Conversion of F0
                to the number of target molecules was obtained by a calibration curve in which
                the log input DNA was related to the log of F0
                 [18]. Subsequently, this equation was used for quantification with log transformation
                of fluorescence data to increase goodness-of-fit as described in Goll et al. 2006 [19].



                
    Description of the Cy0 method
    

                The Cy0 value
                is the intersection point between the abscissa axis and tangent of the inflection
                point of the Richards curve obtained by the non-linear regression of raw data
                (Fig. 1).

                
    
                    

                    
    Figure 1
    
                    Example of modelling PCR amplification with a 5-parameter Richards function
                    Effectiveness of this model is illustrated by the
                    predicted values generated by Eq. 3 (open circles) that agree with the observed
                    fluorescence (dot and line). Curve-fitting of experimentally derived fluorescence
                    dataset to Eq. 3 generates values for the kinetic parameters from which the
                    inflection point (solid black rhombus) and the slope of the curve can be derived.
                    The quantitative entity Cy0 (solid black dot), used in the
                    proposed method, shows the cross point between the x-axis and the tangent crossing
                    the inflection point of real-time PCR fluorescence curve.

                
    


                The Cy0 method was performed by nonlinear regression f
                itting of the Richards function [25], an extension of logistic growth
                curve, in order to fit fluorescence readings to the 5-parameter Richards function:





                
                
    
                    
    
                        
                            

                        
                        Eq. 3
                    
    




                where x is the cycle number, Fx
                is the reaction fluorescence at cycle x,
                Fmax is the maximal
                reaction fluorescence, x is the
                fractional cycle of the turning point of the curve, d represents the Richards coefficient,
                and Fb is the background reaction fluorescence. The inflection point coordinate (Flex)
                was calculated as follows (Additional file 2):

                
                
    
                    
    
                        
                            

                        
                        Eq. 4
                    
    



                and the tangent slope (m) was estimated as:
    

                
                
    
                    
    
                        
                            

                        
                        Eq. 5
                    
    

                When d = 1, the Richards equation becomes the logistic equation shown above.
                The five parameters that characterized each run were used to calculate the Cy0 value by the following
                equation:

                
                
    
                    
    
                        
                            

                        
                        Eq. 6
                    
    

                Although the Cy0 is a single quantitative entity, as is
                the Ct or Cp for threshold methodologies, it accounts for the reaction kinetic
                because it is calculated on the basis of the slope of the inflection point of fluorescence data.
    

                
    Statistical data analysis
    

                Nonlinear regressions (for 4-parameter sigmoid and 5-parameter
                Richards functions) were performed determining unweighted least squares estimates
                of parameters using the Levenberg-Marquardt method. Accuracy was calculated using the
                following equation:


                

                , where

                

                was the relative error, while

                

                and

                


                were the estimated and the true number of DNA molecules for each combination of input DNA
                (nDna) and amplification mix percentage (%mix) used in
                the PCR. Precision was calculated as:
    

                , where


                 was the coefficient of variation,
                 and
                

                were the mean and the standard deviation for each combination of nDna and %mix.
                In order to verity that the Richards curves, obtained by nonlinear regression
                of fluorescence data, were not significantly different from the sigmoidal
                curves, the values of d parameter were compared to the expected value
                d= 1, using t test for one sample. For each combination of
                nDna, %mix, the t values were calculated as follow:
    



                , where

                 and

                

                were the mean and the standard error of d
                values for each combination of nDna
                and %mix, with p(t) < 0.05 for significance level.

                


                values were reported using 3-d scatterplot graphic, a complete second order polinomial
                regression function was shown to estimate the trend of accuracy values.
                 where also reported using 3-d contour
                plots using third-order polynomials spline fitting.
                All elaborations and graphics were obtained using Excel (Microsoft), Statistica
                (Statsoft) and Sigmaplot 10 (Systat Software Inc.).

                
    Results
    

                
    Experimental system 1: reduction of amplification mix percentage
    

                With our experimental set up, the mean PCR reaction
                efficiency was 88% under optimal amplification conditions and slightly
                decreased in the presence of smaller amplification mix up to 84%. Moreover, for
                decreasing amplification mix amounts, the PCR reaction efficiencies showed
                higher dispersion levels than optimal conditions leading to increasing
                quantitative errors (Variation Interval, VI100%= 1.921-1.852 and VI60%=
                1.903-1.776; Fig. 2). Subsequently, the
                fluorescence data obtained in these reactions were used to calculate the
                initial DNA amount using four different procedures: SCF, Ct,
                Cp and Cy0.



                
    Precision and accuracy of the SCF
                    method
    

                Previous studies have shown that the SCF approach can lead to
                quantification without prior knowledge of amplification efficiency  [18, 19, 26];
                therefore, we evaluated the performance of this method on our data set.
                To assess the effect of unequal
                efficiencies on accuracy, the calculated input DNA, expressed as molecular
                number, was compared to the expected value obtaining the relative error (RE). The
                precision was further evaluated measuring the variation coefficient (CV%) of
                the estimated initial DNA in the presence of different PCR efficiencies and input DNA.
    

                In our experimental design, the SCF method showed a very poor precision
                (mean CV% = 594.74%) and low accuracy (mean RE = -5.05). The impact of
                amplification efficiency decline on accuracy was very strong resulting in an
                underestimate of samples of up to 500% (Additional file 3). The log
                transformation of fluorescence data before sigmoidal fitting significantly
                reduced the CV% and RE to 66.12% and -0.20, respectively; however, the overall
                bias remained the same [19]. Finally, we also tested an improved
                SCF approach based on a previous study
                by Rutledge 2004 [26] without obtaining significant
                amelioration (Additional file 4).

                

                
    
                    

                    
    Figure 2
    
                    Estimation of PCR efficiency using LinReg method
                    Efficiency values were determined from 420 independent reactions using a
                    combination of 3.14 x 107 x 3.14 x 101 DNA molecules
                    as starting template and amplification mix quantities ranging from 60% to 100%.
                    The graph shows the distribution of PCR efficiencies in relation to the
                    percentage of amplification mix used in the reaction. The solid black
                    squares (?) represent the mean of each distribution.

                
    


                
    The Cy0 method
    

                The SCF model assumes that the fluorescence signal is
                proportional to the amount of product, which is often the case for SYBR-Green
                I real-time PCR performed with saturing concentrations of dye. In such conditions, centrally
                symmetric amplification curves are expected. However, in our experience, we
                found several non-symmetric amplification curves shown to have good amplification
                efficiency using standard curve analysis (Additional file 1 and 3). In order to
                find a suitable mathematical representation of the complete PCR kinetic curve
                we compared the standard error of estimate obtained by several equations that
                generate S-shaped curves (Tab. 1). As shown in Figure 1, these results
                demonstrated that real-time PCR readouts can be effectively modelled using the 5-parameter
                Richards function (Eq. 3). The Richards equation is an extension of the sigmoidal
                growth curve; specifically, when d
                coefficient is equal to 1, the sigmoidal and Richards curves are the same. Hence,
                we analysed the variation of the d
                coefficient in the presence of different input DNA and PCR efficiencies. Figure
                3 shows that the d value is close to
                1 at amplification mix percentages ranging from 100% to 90% while at lower
                amplification mix contents, where PCR efficiency decreases, the
                d coefficient was significantly higher
                than 1 regardless of the starting DNA content (Fig. 3; Tab. 2). These data
                demonstrate that sigmoidal fitting represents a good approximation of real-time
                PCR kinetic only in the presence of optimal amplification conditions while the
                Richards curve is more suited when PCR is inhibited. Since the Richards growth
                equation includes sigmoidal amplification curves, when d = 1, this nonlinear
                fitting was used in our method.

                

                
    
                    

                    
    Figure 3
    
                    Distribution of Richards coefficients (d) estimated
                        from PCR fluorescence curves using Eq. 3 in nonlinear fitting procedure.
                    Richards coefficient values were determined from 420 independent PCR reactions.
                    The data have been reported in Log10scale, and represented as mean
                    and standard deviation.

                
    

                
    


                    
    Table 1
    
                    Comparison of five S-shaped models to fit the PCR curve:
                        Sigmoid, Richards, Gompertz, Hill and Chapman.
                    In this table, f is the fluorescence at cycle x; Fmax
                        represents the maximum fluorescence value; Fb is
                    the background reaction fluorescence; b, c and d determine the
                    shape of each curve. For each model the determination coefficient (R2),
                    the adjusted determination coefficient (Adj R2) and the standard error
                    of estimate have been calculated.

                    
    
                        
                            
    
                                Name
                                Equation
                                Estimated Parameters
                                R2
                                Adj R2
                                Standard Error of Estimate
                            
    
                            
    
                                
                                
                                
    		
                                
                                
                                
                            
    
                            
    
                                
                                
                                
                                Fmax
                                b
                                c
                                Fb
                                d
                                
                                
                                
                            
    
                            
                        
    
                            Sigmoid
                            f = Fb+Fmax/(1+exp(-(x-c)/b))
                            45.11
                            1.49
                            22.37
                            -0.03
                            
                            1
                            1
                            0.1354
                        
    
                        
    
                            Richards
                            f = Fb+(Fmax/(1+exp(-(1/b)*(x-c)))^d)
                            45.11
                            1.58
                            21.95
                            0.02
                            1.20
                            1
                            1
                            0.0926
                        
    
                        
    
                            Gompertz
                            
                                f = Fb+Fmax *exp(-exp(-(x-c)/b))
                            45.19
                            2.15
                            21.45
                            
                            0.29
                            0.9992
                            0.9992
                            0.6006
                        
    
                        
    
                            Hill
                            
                                f = Fb+Fmax *x^b/(d^b+x^b)
                            45.18
                            14.95
                            
                            0.08
                            22.34
                            1
                            1
                            0.1351
                        
    
                        
    
                            Chapman
                            
                                f = Fb+Fmax *(1-exp(-b*x))^d
                            
                            45.19
                            0.46
                            
                            0.29
                            20615
                            0.9992
                            0.9992
                            0.6006
                        
    

                    
    
                
    

                
                        

                    
    Table 2
    
                    tstatistic values obtained for all variable combinations.
                    When t < 0 the Richards coefficient is lower than 1,
                    while for t > 0 the Richards coefficient is higher than
                    1.
    
                    Significance levels:
    
                    * 0.05 <p < 0.01;
    
                    ** p < 0.01.




                    
    
                        
                            
    
                                
                                Amplification mix percentage
                            
    
                            
    
                                
                                
                                    
    
                                    		
                            
    
                            
    
                                
                                    Log10input DNA
                                
                                100%
                                90%
                                80%
                                70%
                                60%
                            
    
                            
                        
    
                            7.5
                            0.28348
                            1.15431
                            2.9303*
                            5.43493**
                            4.26067**
                        
    
                        
    
                            6.5
                            -3.0233*
                            -0.5329
                            7.8552**
                            8.68609**
                            7.28178**
                        
    
                        
    
                            5.5
                            -2.2195*
                            2.70419*
                            4.7185**
                            8.61406**
                            4.60465**
                        
    
                        
    
                            4.5
                            0.97856
                            1.32162
                            2.34*
                            16.5192**
                            17.5903**
                        
    
                        
    
                            3.5
                            1.00647
                            -1.038
                            2.3307*
                            13.2572**
                            4.65683**
                        
    
                        
    
                            2.5
                            -1.731
                            -0.5995
                            5.8385**
                            6.90378**
                            6.13465**
                        
    
                        
    
                            1.5
                            0.14417
                            1.25452
                            -0.898
                            1.87978
                            3.69668**
                        
    

                    
    

                
    




                Despite the good fitting obtained by
                the Richards equation, the application of kinetic parameters to estimate
                F0 values showed a very low degree
                of precision and accuracy (Additional file 3). In an attempt to increase the
                reproducibility of outcomes a log transformation of fluorescence data was
                performed, however no satisfactory results were obtained (Additional file 3).
                To overcome these problems, we formulated an alternative method for starting
                DNA estimation that defines a new quantitative entity, Cy0. Cy0
                can be considered similar to Ct or Cp but the main advantage of the Cy0 method is that it takes
                into account the kinetic parameters of amplification curve. This new method is
                based on the fit of Eq. 3 to real-time PCR data by nonlinear regression in
                order to obtain the best fit estimators of reaction parameters. In addition,
                these parameters were used to calculate the Cy0
                value using Eq. 6. From a mathematical standpoint, the Cy0 value
                represents the cross point between the x-axis
                and the tangent crossing the inflection point of the real-time PCR fluorescence
                curve. For example, in Figure 4, three real-time PCR quantifications starting
                from the same amount of DNA but in the presence of decreasing amplification mix
                are shown. In these amplification conditions, the Ct method clearly
                underestimated the samples due to the shift
                towards the right of Ct (Fig. 4A). On
                the contrary, using the Cy0
                methods this shift was clearly correct. In fact, in the presence of PCR
                inhibition, the fluorescence values of curve inflection points decreased as did
                the slope of the curve in that point. This resulted in a very small variation
                of Cy0 values (CV% = 0.6%;
                Fig. 4B), while the same fluorescence data analysed by Ct methods produced
                a CV% of 1.45% (Fig. 4A). 
                


                
    
                    

                    
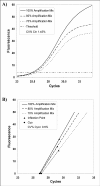
    Figure 4
    
                    Plot of fluorescence observations versus cycle number obtained
                        from the same starting DNA but in presence of decreasing amounts of amplification mix.
                    This slight PCR inhibition produces curves which are less steep than
                    controls and shifted towards the right. When analysed by the threshold method,
                    these curves showed higher Ct values with a CV% of 1.45% (A). An example
                    of Cy0 procedure has been reported for the same data set (B).
                    In this method, the amplification reactions are described by the tangent crossing the
                    inflection point of fluorescence curves. As shown in this figure, the straight-lines
                    originating from PCRs, characterized by slightly different PCR efficiency and the
                    same starting amounts, tend to cross into a common point near the x-axis leading to
                    small variations in the Cy0 values (CV% = 0.6%).

                
    
                
    




                
    Precision and accuracy of the Ct, Cp and Cy0 methods.
    

                The performance of the
                Ct,
                Cp and
                Cy0 methods was compared
                in terms of precision and accuracy over a wide range of input
                DNA concentrations and under different reaction efficiencies obtained by
                decreasing the amount of amplification mix as reported in Liu and Saint [18, 27].
                As shown in Figure 5A, the Ct method is highly rigorous at maximum
                reaction efficiency regardless of the starting DNA template. However, the absolute
                value of RE increased almost linearly with the decrease of efficiency regardless
                of the template concentrations resulting in an underestimation of the unknown of
                about 50% at the lowest amplification efficiencies. The Cp was more accurate
                than the Ct method in the presence of
                different amounts of amplification mix. Indeed, the relative error in the presence
                of 100% amplification mix tended towards zero as it did using the Ct method. However, when the efficiency
                declined, the RE increased initially in the same manner at low and high input
                DNA concentrations, while at 60-70% of the amplification mix, this method
                markedly underestimated at low concentrations (mean RE60% mix; =
                -0.58; Fig. 5C). Finally, the Cy0
                method was more accurate than the Cp
                method (mean RE -0.12 versus -0.18, respectively; Fig. 5C, E), which in turn was
                better than the Ct method (mean RE =
                -0.31). Notably, at optimal amplification conditions (90-100% of the amplification
                mix) the Cp and Cy0 methods were equivalent, but at decreasing
                efficiencies, the Cy0 accuracy
                was more stable than that of the Cp
                in the concentration range from 3.14x107 to 3.14x105 molecules.
                At lower DNA concentrations, from 3.14x104 to 3.14x102 molecules,
                the RE proportionally increased with the efficiency decline, but this underestimate
                was less marked than that of the Cp method
                at the same starting DNA (Fig. 5C, E). Regarding the precision of the three
                methods, the variation coefficients were determined for each combination of
                initial template amount and amplification mix percentage. The random error of
                quantification achieved by the Cp and Cy0 method was similar (mean
                CV% 21.8% and 22.5%, respectively), while the Ct procedure produced an overall
                CV% of about 39.7% (Tab. 3). When
                the CV was analysed in relation to PCR efficiency and input DNA, an area of low
                variation coefficients for the three methods was found between 3.14x104
                and 3.14x107 molecules as starting material (Fig. 5B, D, F). With
                DNA amounts ranging from 3.14x103 to 3.14x102  molecules, the precision progressively
                decreased in each analysis procedure. These variations were not efficiency-dependent,
                but were related to initial DNA quantity as shown by the shapes of level curves
                reported in figure 5B, D and F, which were perpendicular to the input template
                amounts.

                


                
    
                    

                    
    Figure 5
    
                    Comparison of the Ct, Cp and Cy0 methods
                        in terms of precision and accuracy.
                    The accuracy of each method has been reported
                    as Relative Error (RE = expected value ? estimated value) while the precision was
                    evaluated measuring the variation coefficient (CV%). The 3D plots show the variation
                    of relative error in relation to amplification mix percentage and log10 input
                    DNA for the Ct (A), Cp (C) and Cy0 (E) methods.
                    The areas in the level curve graphs represent the CV% values obtained for each amplification
                    mix percentage and Log10 input DNA combination using the Ct (B),
                    Cp (D) and Cy0 (F) methods.

                
    

                
                   

                    
    Table 3
    
                    Comparison of mean Relative Error and mean Variation Coefficient among the Ct, Cp, Cy0 and SCF methods.
                    The reported data were calculated on 420 PCRs except
                    for a) in which the reaction number was 210.

                    
    
                        
                            
    
                                
                                Ct
                                Cp
                                
                                    Cy0
                                
                                SCF
                                
                                    Log10SCF
                                
                            
    
                            
                        
    
                            Mean CV%
                            39.70%
                            21.80%
                            22.52%
                            594.74%a
                            
                            66.12%a
                            
                        
    
                        
    
                            Mean RE
                            -0.318
                            -0.184
                            -0.128
                            -5.058a
                            
                            -0.205a
                            
                        
    
                    
    

                
    




                

                
    Experimental system 2: Real-time PCR quantification in the presence of the inhibitor IgG
    

                The real-time amplification plot of
                4.05x106 DNA molecules with increasing concentrations of IgG
                demonstrates the effects of PCR inhibition on amplification efficiency and
                accumulated fluorescence (Fig. 6A). As inhibitor concentrations increased, the
                amplification curves showed lower plateau fluorescence levels and a shift
                towards the right and the bottom of the inflection points, leading to amplification
                curves that were less steep and not as symmetric as those obtained in absence
                of the inhibitor agent (Fig. 6A). As shown in figure 6A the amplification
                curves inhibited by IgG showed a shape very similar to those resulting from the
                system of amplification mix reduction (system 1; Fig. 4A). Quantitative data
                analysis of these amplification plots showed that the estimated DNA quantities
                were systematically underestimated in the presence of IgG concentrations higher
                than 0.25 µg/ml and 1 µg/ml using Ct and Cp methods,
                respectively. However, the Cy0
                method was able to adjust this bias minimizing the RE at high IgG
                concentrations (RE = 4.98%; CV = 4.33%; Fig. 6B).

  
                Furthermore, in presence of
                high IgG concentrations, the SCF
                approach, modified according to Rutledge 2004 [26], was inapplicable because it was
                impossible to minimize F0
                value (Additional file 5).
    



                
    Discussion
    

                None of the current quantitative PCR
                data treatment methods is in fact fully assumption-free, and their statistical
                reliability are often poorly characterized. In this study, we evaluated whether
                known real-time elaboration methods could estimate the amount of DNA in
                biological samples with precision and accuracy when reaction efficiencies of the
                unknown are different from those of the standard curve.
    

                Our experimental systems consisted
                in the quantification of samples with the same known starting template amount
                but the amplification reaction, performed for the real-time PCR assay, had a slightly
                decreasing efficiency. This is clearly not in agreement with the main assumption
                of the threshold approach which holds that the amplification efficiency of
                samples has to be identical to, or not significantly different from, that
                predicted by the standard curve. However, such an assumption has been reported
                to be patently invalid for many cases in medical diagnostics. In fact, some, if
                not all, of the biological samples may contain inhibitors that are not present
                in the standard nucleic acid samples used to construct the calibration curve,
                leading to an underestimation of the DNA quantities in the unknown samples [28, 29].
    
                In our study, slightly decreasing
                efficiencies were obtained by two systems: diluting the master enzyme mix or
                adding IgG, a known inhibitor of PCR. Although, the first system is
                an  "in vitro" simulation of PCR inhibition, it produces
                amplification curves very similar to those obtained in the presence of a
                biological inhibitor like IgG.
    

                Notably, our experimental setup is
                not characterized by aberrant amplification reactions. On the contrary, the
                reactions show a slight mean efficiency decrease which is always the case of
                biological samples. This PCR inhibition remains undetected when using a
                threshold approach leading to target underestimation. Moreover, small
                differences in amplification efficiency produce large quantitative errors and
                the frequency and magnitude of these errors are virtually impossible to
                ascertain using a threshold approach. It has been shown that a difference as
                small as 4% in PCR efficiency could translate into a 400% error in
                comparative Ct method based quantification [24].
    

                Considering previous works [18, 19] which demonstrated the capability
                of the SCF method to quantify a sample without prior knowledge of amplification
                efficiency, our first choice was to process the experimental data by the SCF
                method. The effectiveness of the SCF
                approach is based on curve fitting of raw data so that variations unique to
                each amplification reaction are incorporated into the analysis. Hence, the
                results reported herein surprisingly demonstrated that the accuracy and
                precision of the SCF method was markedly
                impaired when efficiency fell. In fact, when PCR efficiency decreased by about
                2.5% (88.8% efficiency value in the presence of 100% of the amplification mix
                dropped to 84.4% efficiency in the presence of 60% of the mix), we observed,
                using the SCF method with
                log-transformation, that the RE and CV went from 15% to 43% and from 61% to
                55%, respectively.
    

                Furthermore, we found that, when the
                amplification curve was inhibited, by IgG, the method proposed by Rutledge [26] can not be applied because for each
                cut-off cycle eliminated from the plateau phase the F0 value progressively
                decreased without ever reaching a
                minimum value. These observations are in agreement with two recent studies, which
                reported that it is possible to obtain absolute quantification from real-time
                data without a standard curve, but the Ct
                method remains a gold standard due to the inherent errors of the multiple
                estimates used in nonlinear regression [19, 20]. These observations are in
                accordance with Feller ' s conclusions that different S-shaped curves
                can be effectively fitted with various sigmoid models [30], each providing
                distinct F0 values. Thus sigmoid fit
                methods such as the logistic model, used in the SCF approach, are purely
                descriptive and quantitative results may
                be unreliable. This led us to develop a new mathematical data treatment method,
                named Cy0, based on
                nonlinear regression fitting of real-time fluorescence data. The proposed
                method ' s main advantages are its use of the Richards equation for obtaining
                the coordinate of the inflection point and the determination of the
                quantitative entity Cy0 using
                the five parameters of reaction curve.
    

                Although the logistic growth
                equation generates a curve that tends towards an exponential form at low
                fluorescence values, making this curve ideal to model PCR reaction, its maximum
                slope, or inflection point, is always imposed to be at half the value of the
                upper asymptote, (Fmax-Fb)/2. This is unsatisfactory
                because the factors that determine the growth rate are complex and some
                amplification systems, although characterized by good reaction efficiency, as
                assessed by standard curve, do not have the center of symmetry in the inflection
                point. The Richards equation is a more flexible growth function because it has
                an additional parameter, which is a shape parameter that can make the Richards
                equation equivalent to the logistic, Gompertz, or monomolecular equations [31].
                Variation of the shape parameter
                allows the point of inflection of the curve to be at any value between the
                minimum and the upper asymptote; when d
                = 1 the Eq. 3 becomes the sigmoidal equation.
    

                Furthermore, since very small errors
                of the multiple estimates used in non-linear regression lead to large
                variations in F0 values,
                the real-time PCR kinetic parameters were used to define a new quantitative
                entity, the Cy0. The Cy0 relies on the inflection point
                position and on the slope of the fluorescence curve at that point, so that its
                value slightly changes in relation to PCR efficiency. In particular, in a slightly
                inhibited amplification reaction, the fluorescence curves are shifted towards the
                right and/or they are less steep; this generates higher Ct values than those
                found under optimal amplification conditions,
                underestimating the target amount. In the Cy0
                method, the tangents, calculated from different PCR efficiency, tend to
                intersect at a common point near the x-axis leading to small variations in the Cy0 values (Fig. 4).
    




                The standard curve approach was
                chosen for the proposed method because currently there no genuine mathematical
                model for PCR efficiency assessment. The main complication is that actual
                efficiency amplification is not constant through the PCR run being high in
                exponential phase and gradually declining towards the plateau phase [33, 35].
                However, most current methods of PCR efficiency assessment report "overall"
                efficiency as a single value [13, 24, 36, 37].
                Moreover, recent publications on PCR efficiency assessment have concentrated on the analysis of individual shapes
                of fluorescence plots in order to estimate a dynamic efficiency value [19, 20, 27, 38].
                This proliferation of new methods
                to assess PCR efficiency demonstrates that, at present, there is not an
                accepted procedure to evaluate PCR efficiency from a single run, hence some
                methods can "overestimate" and others "underestimate" the "true" PCR efficiency [8].
                In contrast, the standard curve method is based on a simple approximation of data obtained in standard
                dilutions to unknown samples. In this procedure PCR efficiency assessment is
                based on the slope of the standard curve. Indeed, the original method
                (Ct) does not account for PCR efficiencies in individual target samples.
                The proposed procedure overcomes this limitation by evaluating single amplification variations using Richards
                curve fitting and subsequently produces a Cy0
                value that minimizes the dependence of its value on PCR kinetic.
    

                We then compared our method with the
                Ct method, the actual "gold standard" in
                real-time PCR quantification and the Cp method which is also used in
                molecular diagnostics. Both methods are based on standard curve methodology and
                are the most frequently used in this field. The Ct, Cp and Cy0 methods were evaluated on
                the same data set using two criteria: precision and accuracy. We defined the accuracy
                of a model as its ability to provide expected concentrations of the known dilutions
                under different PCR amplification efficiencies. On the contrary, precision is
                related to the variability of the results obtained from a given model, and it
                indicates whether reliable results may be obtained from a small data
                collection. Our results clearly demonstrated that, under optimal amplification
                conditions, these three methods were equally precise and accurate. However, when
                the PCR efficiency decreased, due to amplification mix dilution or IgG
                presence, the Ct method was markedly
                impaired and the Cp and Cy0 methods proved to be
                significantly more accurate than the Ct
                method. Notably, the Cy0
                method showed accuracy levels higher than the Cp method maintaining
                the same precision.
    

                The ability to carry out reliable
                nuclei acid quantification even in sub-optimal amplification conditions is particularly
                useful when PCR optimization is not possible, as in the case of high-throughput
                screening of gene expression or biological samples difficult to cleanse of PCR
                inhibitors.
    

                Furthermore, the Cy0 method is completely objective
                and assumption-free. Indeed, it does not require the choice of a threshold
                value and the assumption of similar amplification efficiency between the
                standard curve and biological samples, necessary in the Ct method.
                Moreover, there is no need to assume that base pair
                composition and amplicon size do not impact the fluorescence characteristics of
                SYBR Green I, required in optical calibration methods like SCF [19].
                Our procedure may have future
                applications in TaqMan assays, where the Taq DNA polymerase digests a probe
                labelled with a fluorescent reporter and quencher dye and the signal diverges
                from the product resulting in non-symmetric amplification curves that can be effectively
                modelled by Richards equation [39]. Further work is needed to
                extensively verify the accuracy and precision of the Cy0 method
                in the presence of other known PCR inhibitors
                like phenol, haemoglobin, fat and tannic acid [17, 22].

                


                
    
                    

                    
    Figure 6
    
                    Real-time PCR amplification plots obtained from the same starting
                        DNA in the presence of IgG acting as reaction inhibitor
                    This inhibition system
                    produces curves which are progressively less steep than non-inhibited reactions with
                    increasing IgG concentrations (A). When analysed by the Ct, Cp and
                    Cy0 methods these curves showed a RE% of -25.37%, -9.02%
                    and 4.98% and a CV% of 25.62%, 10.66% and 4.33%%, respectively (B).

                
    


                
    Conclusions
    

                Real-time PCR analysis is becoming
                increasingly important in biomedical research because of its accuracy,
                sensitivity and high efficiency. Although, real-time PCR analysis has gained
                considerable attention, it is far from being a standard assay. The standard
                methods are quite stable and straightforward but the accuracy of estimates is
                strongly impaired if efficiency is not equal in all reactions. Furthermore, the
                assumption of uniform efficiency has been reported to be invalid in many cases regarding
                medical diagnostics. In fact, the biological samples may contain inhibitors
                that could lead to different amplification efficiencies among samples.
    

                We propose, in this report, a modified
                standard curve-based method, called Cy0,
                that does not require the assumption of uniform reaction efficiency between
                standards and unknown.

                To the best of our knowledge, this
                is the first method in which the stability and reliability of a standard curve
                approach is combined with a fitting procedure to overcome the key problem of
                PCR efficiency determination in real-time PCR nucleic acid quantification. The
                data reported herein clearly show that the Cy0
                method is a valid alternative to the standard method for obtaining reliable and
                precise nucleic acid quantification even in sub-optimal amplification
                conditions, such as those found in the presence of biological inhibitors like
                IgG.

                
    

                
    List of abbreviations used
    

                Cp: crossing point; Ct: threshold
                cycle; CV: coefficient of variation; IgG: immunoglobulin G; RE: relative error;
                SCF: sigmoidal curve fitting.
    

                
    Authors' contributions
    

                MG and DS carried out the design of
                the study, participated in data analysis, developed the Cy0 method and drafted the manuscript. MBLR participated
                in data collection and analysis and critically revised the manuscript. LS
                carried out the real-time PCR. VS participated in the design of the study and
                critically revised the manuscript. All authors read and approved the final
                manuscript.
    

                
    Acknowledgements
    

                We thank Dr. Pasquale Tibollo for
                technical assistance and Dr. Giosué Annibalini for helpful comments on the
                manuscript.
    

                
    

                    
    References
    

                    
    
                        1. Higuchi R, Fockler C, Dollinger G, Watson R:
                        Kinetic PCR analysis: real-time monitoring of DNA amplification reactions. Biotechnology (N Y) 1993,
                        11(9):1026-1030.
    

                    
    
                        2. Schmittgen TD:
                        Real-time quantitative PCR. Methods 2001,
                        25(4):383-385.
    

                    
    
                        3. Bustin SA, Nolan T:
                        Pitfalls of quantitative real-time reverse-transcription polymerase chain reaction.
                        J Biomol Tech 2004, 15(3):155-166.
    

                    
    
                        4. Gingeras TR, Higuchi R, Kricka LJ, Lo YM, Wittwer CT:
                        Fifty years of molecular (DNA/RNA) diagnostics. Clin Chem 2005, 51(3):661-671.
    

                    
    
                        5. Bustin SA, Mueller R:
                        Real-time reverse transcription PCR (qRT-PCR) and its potential use in clinical diagnosis. Clin Sci (Lond) 2005,
                        109(4):365-379.
    

                    
    
                        6. Nolan T, Hands RE, Bustin SA:
                        Quantification of mRNA using real-time RT-PCR. Nature
                            Protocols 2006, 1(3):1559-1582.
    

                    
    
                        7. Marubini E, Verderio P, Raggi CC, Pazzagli M, Orlando C:
                        Statistical diagnostics emerging from external quality control of real-time PCR.
                        The International journal of biological markers 2004, 19(2):141-146.
    

                    
    
                        8. Pfaffl M:
                        Quantification strategies in real time PCR. In A-Z of quantitative PCR
                            Edited by: Bustin SA La Jolla, CA, International University Line 2004.
    

                    
    
                        9. Luu-The V, Paquet N, Calvo E, Cumps J:
                        Improved real-time RT-PCR method for high-throughput measurements using second
                            derivative calculation and double correction. BioTechniques 2005, 38(2):287-293.
    

                    
    
                        10. Livak KJ: ABI Prism 7700 sequence detection system. User Bulletin 2. PE Applied
                            Biosystems 1997.
    

                    
    
                        11. Rutledge RG, Cote C: Mathematics of quantitative kinetic PCR and the application of standard curves.
                        Nucleic Acids Res 2003, 31(16):e93.
    

                    
    
                        12. Raeymaekers L: A commentary on the practical applications of competitive PCR.
                        Genome Res 1995, 5(1):91-94.
    

                    
    
                        13. Bar T, Stahlberg A, Muszta A, Kubista M:
                        Kinetic Outlier Detection (KOD) in real-time PCR. Nucleic Acids Res 2003, 31(17):e105.
    

                    
    
                        14. Lefevre J, Hankins C, Pourreaux K, Voyer H, Coutlee F: Prevalence of selective inhibition of HPV-16 DNA amplification in
                            cervicovaginal lavages. Journal of
                            medical virology 2004, 72(1):132-137.
    

                    
    15. Sunen
                        E, Casas N, Moreno B, Zigorraga C: Comparison
                            of two methods for the detection of hepatitis A virus in clam samples (Tapes
                            spp.) by reverse transcription-nested PCR. International journal of food microbiology 2004, 91(2):147-154.
    

                    
    16. Jiang
                        J, Alderisio KA, Singh A, Xiao L: Development
                            of procedures for direct extraction of Cryptosporidium DNA from water
                            concentrates and for relief of PCR inhibitors. Applied and environmental microbiology 2005, 71(3):1135-1141.
    

                    
    17. Kontanis
                        EJ, Reed FA: Evaluation of real-time PCR
                            amplification efficiencies to detect PCR inhibitors. J Forensic Sci 2006, 51(4):795-804.
    

                    
    18. Liu
                        W, Saint DA: Validation of a
                            quantitative method for real time PCR kinetics. Biochem Biophys Res Commun 2002, 294(2):347-353.
    

                    
    19. Goll
                        R, Olsen T, Cui G, Florholmen J: Evaluation
                            of absolute quantitation by nonlinear regression in probe-based real-time PCR.
                        BMC Bioinformatics 2006, 7:107.
    

                    
    20. Karlen
                        Y, McNair A, Perseguers S, Mazza C, Mermod N: Statistical significance of quantitative PCR. BMC Bioinformatics 2007, 8:131.
    

                    
    21. Bustin
                        SA: Absolute quantification of mRNA
                            using real-time reverse transcription polymerase chain reaction assays. J Mol Endocrinol 2000, 25(2):169-193.
    

                    
    22. Tichopad
                        A, Didier A, Pfaffl MW: Inhibition of
                            real-time RT-PCR quantification due to tissue-specific contaminants. Mol Cell Probes 2004, 18(1):45-50.
    

                    
    23. Nolan
                        T, Hands RE, Ogunkolade W, Bustin SA: SPUD:
                            a quantitative PCR assay for the detection of inhibitors in nucleic acid
                            preparations. Anal Biochem 2006, 351(2):308-310.
    

                    
    24. Ramakers
                        C, Ruijter JM, Deprez RH, Moorman AF: Assumption-free
                            analysis of quantitative real-time polymerase chain reaction (PCR) data. Neurosci Lett 2003, 339(1):62-66.
    

                    
    25. Richards
                        F: A flexible growth function for
                            empirical use. Journal of
                            experimental Botany 1959, 10:290-300.
    

                    
    26. Rutledge
                        RG: Sigmoidal curve-fitting redefines
                            quantitative real-time PCR with the prospective of developing automated
                            high-throughput applications. Nucleic
                            Acids Res 2004, 32(22):e178.
    

                    
    27. Alvarez
                        MJ, Vila-Ortiz GJ, Salibe MC, Podhajcer OL, Pitossi FJ: Model based analysis of real-time PCR data from DNA binding dye
                            protocols. BMC Bioinformatics 2007,
                        8(1):85.
    

                    
    28. Meijerink
                        J, Mandigers C, van de Locht L, Tonnissen E, Goodsaid F, Raemaekers J: A novel method to compensate for different
                            amplification efficiencies between patient DNA samples in quantitative
                            real-time PCR. J Mol Diagn 2001, 3(2):55-61.
    

                    
    29. Stahlberg
                        A, Aman P, Ridell B, Mostad P, Kubista M: Quantitative
                            real-time PCR method for detection of B-lymphocyte monoclonality by comparison
                            of kappa and lambda immunoglobulin light chain expression. Clin Chem 2003, 49(1):51-59.
    

                    
    30. Feller
                        W: On the logistic law of growth and its
                            empirical verification in biology. Acta
                            Bioth Ser A 1940(2):51-66.
    

                    
    31. Birch
                        C: A new generalized logistic sigmoid
                            growth equation compared with the Richards growth equation. Annals of Botany 1999, 83:713-723.
    

                    
    32. Yin
                        X, Goudriaan J, Lantinga EA, Vos J, Spiertz HJ: A flexible sigmoid function of determinate growth. Ann Bot (Lond) 2003, 91(3):361-371.
    

                    
    33. Lalam
                        N: Estimation of the reaction efficiency
                            in polymerase chain reaction. J Theor
                            Biol 2006, 242(4):947-953.
    

                    
    34. Zhao
                        S, Fernald RD: Comprehensive algorithm
                            for quantitative real-time polymerase chain reaction. J Comput Biol 2005, 12(8):1047-1064.
    

                    
    35. Gevertz
                        JL, Dunn SM, Roth CM: Mathematical model
                            of real-time PCR kinetics. Biotechnol
                            Bioeng 2005, 92(3):346-355.
    

                    
    36. Peirson
                        SN, Butler JN, Foster RG: Experimental
                            validation of novel and conventional approaches to quantitative real-time PCR
                            data analysis. Nucleic Acids Res 2003,
                        31(14):e73.
    

                    
    37. Tichopad
                        A, Dilger M, Schwarz G, Pfaffl MW: Standardized
                            determination of real-time PCR efficiency from a single reaction set-up. Nucleic Acids Res 2003, 31(20):e122.
    

                    
    38. Liu
                        W, Saint DA: A new quantitative method
                            of real time reverse transcription polymerase chain reaction assay based on
                            simulation of polymerase chain reaction kinetics. Anal Biochem 2002, 302(1):52-59.
    

                    
    39. Livak
                        KJ, Flood, S.J., Marmaro, J., Giusti, W., Deetz, K.: Oligonucleotides with fluorescent dyes at opposite ends provide a
                            quenched probe system useful for detecting PCR product and nucleic acid
                            hybridization. PCR Methods appl 1995,
                        4:357-362.
    
                    
    
                
    

                
    Supplementary Material
    

                
    

                    
    
                        
                            Additional file 1 - 
    
                        Windows Excel file containing PCR readouts and non-linear fittings.
                    
    
                    
    
                        
                            Additional file 2 - 
    
                        Windows Word file containing first and second derivative of Richards
                        equation and the mathematical formulas for obtaining the coordinate of
                        the Cy0 point.
                    
    
                    
    
                        
                            Additional file 3 - 
    
                        Windows Excel file containing the Ct Cp Cy0 SCF Log10 SCF elaborations.
                    
    
                    
    
                        
                            Additional file 4 - 
    
                        Windows Excel file containing the results obtained with the SCF approach based on a previous study by Rutledge 2004.
                    
    
                    
    
                        
                            Additional file 5 - 
    
                        Windows Excel file containing the results obtained with the SCF approach based on a previous study by Rutledge 2004 in presence of IgG.